Métodos de Elementos Finitos Mixtos y Técnicas afines para modelos matemáticos en dinámica de fluidos.

Investigador

Dr. Mario Álvarez Guadamuz

Descripción

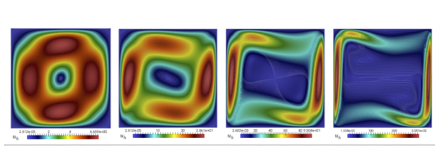
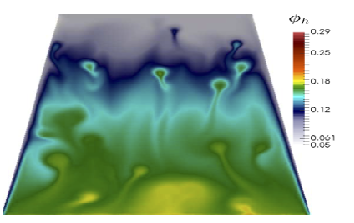
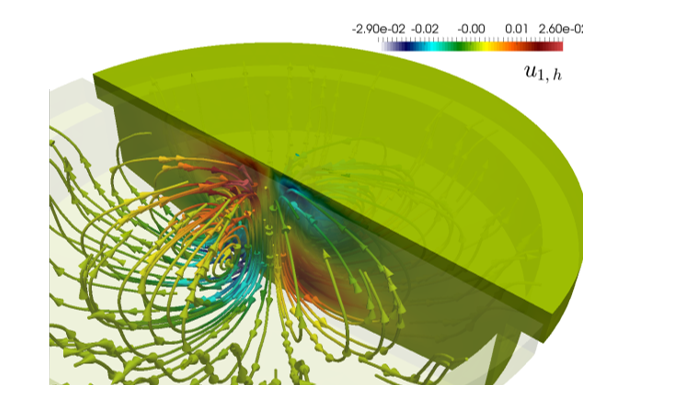
Este proyecto de investigación está orientado al desarrollo de métodos numéricos para simular numéricamente flujos incompresibles con transferencia simultánea de calor y masa en el marco de aproximación de Oberbeck-Boussinesq; un modelo constituido por un sistema tipo Navier-Stokes no linealmente acoplado con ecuaciones de advección-difusion que describen el transporte de la temperatura y la concentración de una cierta sustancia en un fluido viscoso e incompresible. Este modelo matemático permite modelar muchos fenómenos de interés en dinámica de fluidos que tienen diversas aplicaciones prácticas en la industria y en las ciencias aplicadas. Por mencionar sólo algunos ejemplos, en la ingeniería ambiental un conocimiento preciso del mecanismo de transporte de un contaminante es fundamental para determinar su impacto en ciertos ecosistemas. En la industria eléctrica y electrónica, por su parte, se desarrollan componentes de regulación térmica para equipos industriales con base en mecanismos de transferencia de calor espontánea a través de fluidos que son accionados térmicamente. El modelo Oberbeck-Boussinesq permite estudiar la dinámica subyacente de los fenómenos anteriores pero tiene la dificultad de ser sumamente complicado de resolver debido a las no-linealidades y acoplamientos presentes. A raíz de lo anterior, en ésta investigación se busca abordar diversos aspectos matemáticos y numéricos de los métodos mixtos y técnicas a fines para resolver las dificultades mencionadas del modelo en cuestión, y de esta manera poder cuantificar variables físicamente relevantes e inherentes al fenómeno considerado para la descripción posterior del mismo a nivel computacional.

Periodo de investigación:  enero 2020 a diciembre 2022